Crystal Field Stabilisation Energy
(CFSE)
A consequence of Crystal Field Theory is that the distribution
of electrons in the d orbitals can lead to stabilisation for some
electron configurations.
It is a simple matter to calculate this stabilisation since
all that is needed is the electron configuration.
For an octahedral complex, an electron in the more stable
t2g subset is treated as contributing -2/5Δ
whereas an electron in the higher energy
eg subset contributes to a destabilisation of
+3/5Δ.
The final answer is then expressed as a multiple of the
crystal field splitting parameter Δ (Delta).
Based on this, the Crystal Field Stabilisation Energies for
d0 to d10 configurations can then be used
to calculate the Octahedral Site Preference Energies, which is
defined as: OSPE = CFSE (oct) - CFSE (tet)
Note: the conversion between Δoct and
Δtet used for these calculations
is:
Δtet = Δoct * 4/9
Crystal Field Stabilisation Energies
(CFSE)
and Octahedral Site Preference Energies (OSPE)
| Total d-electrons |
Octahedral |
� |
Tetrahedral |
� |
OSPE |
| � |
configuration |
CFSE |
configuration |
CFSE |
� |
| d0 |
t2g0 |
0 Δo |
e0 |
0 Δt |
0 Δo |
| d1 |
t2g1 |
-2/5 Δo |
e1 |
-3/5 Δt |
-6/45 Δo |
| d2 |
t2g2 |
-4/5 Δo |
e2 |
-6/5 Δt |
-12/45 Δo |
| d3 |
t2g3 |
-6/5 Δo |
e2t21 |
-4/5 Δt |
-38/45 Δo |
| d4 |
t2g3eg1 |
-3/5 Δo |
e2t22 |
-2/5 Δt |
-19/45 Δo |
| d5 |
t2g3eg2 |
0 Δo |
e2t23 |
0 Δt |
0 Δo |
| d6 |
t2g4eg2 |
-2/5 Δo + P |
e3t23 |
-3/5 Δt + P |
-6/45 Δo |
| d7 |
t2g5eg2 |
-4/5 Δo + 2P |
e4t23 |
-6/5 Δt + 2P |
-12/45 Δo |
| d8 |
t2g6eg2 |
-6/5 Δo + 3P |
e4t24 |
-4/5 Δt + 3P |
-38/45 Δo |
| d9 |
t2g6eg3 |
-3/5 Δo + 4P |
e4t25 |
-2/5 Δt + 4P |
-19/45 Δo |
| d10 |
t2g6eg4� |
0 Δo |
e4t26 |
0 Δt |
0 Δo |
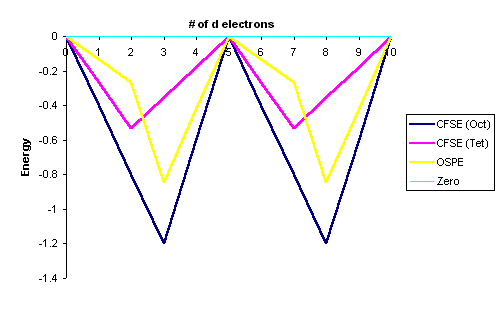
Graphically this can be represented by:
This "double-humped" curve is found for various properties of the first-row
transition metals, including Hydration and Lattice energies of the M(II) ions,
ionic radii as well as the stability of M(II) complexes.
This suggests that these properties are somehow related to Crystal Field effects.
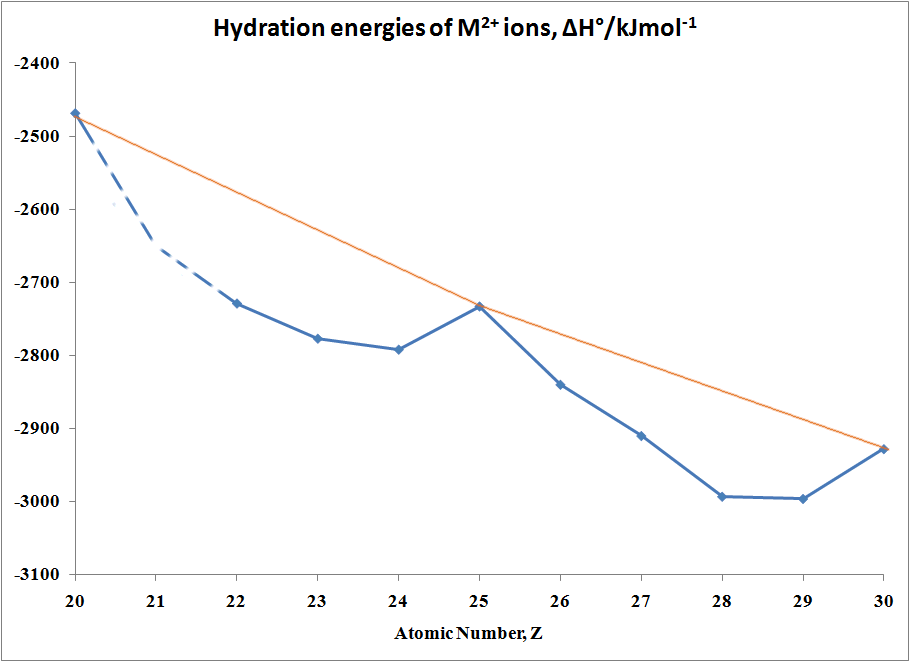
In the case of Hydration Energies,
M2+(g) + H2O →
[M(OH2)6]2+(aq)
the following Table and graph shows
this type of curve. Note that in any series of this type not all
the data are available since a number of ions are not very stable in the
M(II) state.
Table of hydration energies of M2+ ions
| M |
ΔH°/kJmol-1 |
M |
ΔH°/kJmol-1 |
| Ca |
-2469 |
Fe |
-2840 |
| Sc |
no stable 2+ ion |
Co |
-2910 |
| Ti |
-2729 |
Ni |
-2993 |
| >V |
-2777 |
Cu |
-2996 |
| Cr |
-2792 |
Zn |
-2928 |
| Mn |
-2733 |
|
|
Site preferences in Spinels
The mineral MgAl2O4 is known as
spinel. The structure of
which can be described as a cubic close-packed array of oxide ions, between
which are tetrahedral and octahedral holes. The placement of M(II) and M(III)
ions in these holes fit into two schemes: normal spinels and inverse spinels.
Many transition metal ion oxides form spinel type structures of the type
AB2O4 or B3O4 where in the latter
case the metal exists with the oxidation numbers of +2,+3, +3.
In normal spinels the M(II) ions occupy some of the tetrahedral holes
while the M(III) ions occupy some of the octahedral holes.
In inverse spinels, the M(II) ions can be thought of as having swapped with
half of the M(III) ions so that the M(II) are in octahedral holes while
half the M(III) are now in tetrahedral holes with the other half of the M(III)
ions still occupying octahedral holes.
OSPE calculations can be used to correctly predict whether the structure of most
spinels containing transition metal ions will be normal or inverse.
return to the CHEM2101 (C21J) course
outline
Return to Chemistry, UWI-Mona,
Home Page
Copyright © 1998-2010 by Robert John
Lancashire, all rights reserved.
Created and maintained by Prof. Robert J.
Lancashire,
The Department of Chemistry, University of the West Indies,
Mona Campus, Kingston 7, Jamaica.
Created December 1998. Links checked and/or last
modified 13th September 2010.
URL
http://wwwchem.uwimona.edu.jm/courses/CFSE.html
